This week we worked on predictive aim. The player enjoys a bit of assisted aim and AI uses it to shoot at the player. Ballistic weapons use it (that is, weapons that shoot projectiles, unlike lasers or missiles). 

Our first solution was an heuristic: measure the distance between the target and the muzzle, find the time the bullet would take to get there, then find where the target would be after that time and shoot at that position. But we knew there must be a mathematical solution!

After a few google searches we found that the cosine theorem was a nice way to solve this problem. Not easy, though - our maths are a bit rusty! (shame!) The whole thing turns into a quadratic formula we were not able to solve. However, thanks to this article in Gamasutra we got the solution.

More or less, this is the problem we aim (ha!) to solve:

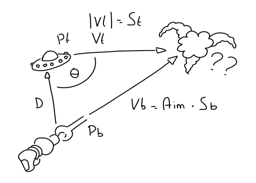
So we have:

• Muzzle: bullet's start position
• Target: target's position
• D: distance from muzzle to target
• Ev: target velocity
• St: target speed - so module of Ev
• theta: angle between vectors target's velocity - muzzle towards target
• Sb: projectile speeed

We know all those things, we want to know t, the time of impact - so we can predict where the target WILL be. We need:

• cos(theta): well, the cosine of theta
• a = 2 · D^2 · St · cos(theta)
• sqrtInner = a^2 + 4 * (Sb^2 - St^2) · D^2

 If sqrtInner or cos(theta) are less than zero there's no solution! Otherwise we can compute two times:

 t1 = (-2 * D * St * cosTheta + Mathf.Sqrt(sqrtInner)) / (2 * (Sb^2 - St^2));
 t2 = (-2 * D * St * cosTheta - Mathf.Sqrt(sqrtInner)) / (2 * (Sb ^2 - St^2));

We can discard t1 or t2 if they are lower than zero. Otherwise we use the smaller of those values (maybe the maximum is useful too, it seems. In our tests, it's safe to stick with the maximum value between t1 and t2.

So, finally, the predicted target position is:

v = Ev + ((targetPosition - muzzle) / Mathf.Max(t1, t2));
expectedTargetPosition = muzzle + v;

And that's it! PEW PEW PEW! We have uploaded a new build where we can test all this fighting a bunch of PeaShooters (basic creatures that fly in front of you and shoot relatively slow projectiles). Fighting against one is easy, but press M to spawn a few more and it becomes quite a challenge...

Try it and share your thoughts!